Mayo

CLASE # 5

Lunes , 2 de mayo del 2016

En esta clase , se reviso el documento La encuesta como técnica de investigación , mientras se realizaba la lectura  la maestra explicaba  detalladamente  acerca de los tipos de preguntas que existen para elaborar una encuesta , se expusieron algunos ejemplos y sugerencias para la correcta elaboracion del proyecto respecto al tema ya mencionado , a continuación una imagen con el contenido que se estudio en clase:

Recuperada de ::https://www.google.com.eckaW5vr_MAhWHMyYKHejvCv8Q_AUIBigB#tbm=isch&q=tipos+de+preguntas+para+una+encuesta&imgrc=rvCXntuZl9V0IM%3A.

Posterior a esto la maestra procedió a realizar la revisión del tema de investigación y objetivos de algunos compañeros , con el fin de hacer algunas correcciones y emitir recomendaciones que contribuyan a la elaboracion de un buen proyecto.

CLASE # 6 

Miércoles , 4 de mayo del 2016

En esta sesión de clases iniciamos propiamente el estudio de la estadística , para ello se revisaron conceptos básicos e importantes , como la definición de estadística y la estadística descriptiva  , mas a profundidad se estudiaron conceptos y procedimientos descritos continuación :

1) Recopilación de datos: 

• Se puede obtener mediante fuentes como entidades gubernamentales , organizaciones , encuestas y entrevistas realizadas .
• También se puede recolectar datos mediante la creación de una encuesta y su aplicación .

2) Simbologia:

• Se denota N al tamaño de la población.
• Se denota n al tamaño de la muestra.
• X: representa a la característica de interés.
• x: Representa al valor de la caracteristica de interés.

3) Descripción del conjunto de datos:

• Tabulación.
• Gráfica.
• Numero que caracteriza al conjunto de datos.

4) Procedimiento para elaborar una tabla de frecuencias>

• Identificar la unidad de medida de los datos.
• Seleccionar el numero de clases o intervalos.
• Determinar la longitud de clase .
• Realizar el centro de datos para obtener la frecuencia en cada clase .
• Organizar informacion en la tabla de frecuencias.

En base a estos parámetros se realizo un ejercicio de aplicación en el cual se construyo la tabla de frecuencias y se procedió a  realizar la gráfica denominada histograma de frecuencias.

Anexos:

Histograma:

 

CLASE # 7

Lunes , 9 de mayo del 2016

En esta clase realizada en el laboratorio de computación , se realizo el estudio de las gráficas que sirven para representar datos cualitativos , siendo estas :

• Gráfico de barras.
• Gráfico circular o pastel.

En base a esto se realizo un ejemplo practico en que se determino las frecuencias absoluta y relativa , se categorizó los datos y se determino los sectores para dibujar el pastel mediante ángulos encontrados empleando una regla de 3 , al final se procedió a realizar la descripción de los gráficos e interpretación de resultados.

Gráficas de barras y pastel:

Luego de estudiar la representación de datos cualitativos , se ejecuto un ejemplo empleando una hoja de calculo de google-drive , en la cual elaboramos una tabla de frecuencias y el histograma respectivo en base a un conjunto de datos propios de un ejemplo.

CLASE # 8

Miércoles , 11 de mayo del 2016

En esta clase se estudiaron mas gráficas referentes a la estadística como la ojiva , el polígono de frecuencias , diagrama de puntos (representa datos cualitativos individuales) ,  el diagrama tallo-hoja y el diagrama de Pareto ; considerando tales se ejecutaron ejemplos de aplicación , para representar los resultados mediante distintas gráficas y aprender a interpretar y describir cada una de ellas , así como su importancia y disponibilidad según la conveniencia del investigador.

Anexos:

Polígono de frecuencias y ojiva.

Diagrama de puntos y diagrama tallo-hoja.

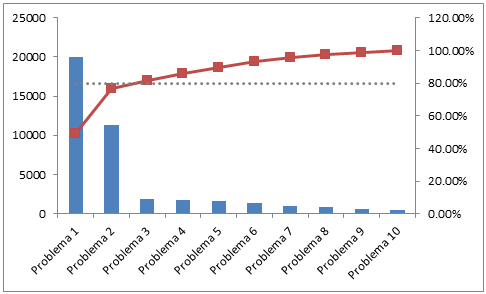
Diagrama de Pareto.

CLASE # 9 

Lunes , 16 de mayo del 2016

En este día se culmino la actividad en clase relacionada a un problema en el que se tenían que procesar los datos proporcionados mediante una tabla de frecuencias y posteriormente representarlos por medio de un histograma , una ojiva , un diagrama de puntos y un diagrama de tallo y hojas ; cada uno con su respectiva descripción e interpretación. El polígono de frecuencias no se lo pudo realizar pues no  se encontró la opción en la hoja de calculo que permitiera gratificarlo.

A mas de terminar lo mencionado , la profesora emitió algunas criticas y recomendaciones con respecto a la elaboracion del cuestionario , la selección de la población y la muestra. Etapas correspondiente al proyecto estadístico establecido.

CLASE # 10 

Miércoles , 18 de mayo del 2016

En dicha clase estudiamos el tema : Calculo de medidas para datos cuantitativos ; excepto la Moda (Mo) 

Este tipo de cálculos como su nombre lo dice están relacionados con un conjunto de  datos estrictamente de carácter cuantitativo , es decir numéricos ; destacan diferentes tipos , entre los mas importantes se tienen los siguientes:

1) Calculo de medidas de localización :

-Media muestral o Promedio : Consiste en sumar todos los datos y el resultado obtenido dividirlo para el numero total de los mimos. Existen diferentes formas para el calculo del promedio y consideramos la manera en la que se encuentren dispuestos los datos.

• Datos individuales : Se calcula empleando al formula:

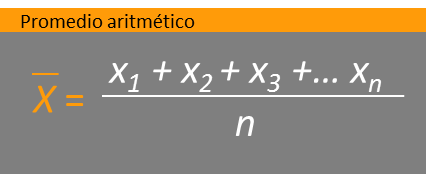
• Datos individuales con frecuencias : Se calcula con la formula:

• Datos agrupados con intervalos : En este caso se aplica la siguiente formula :

-Mediana muestral : La mediana en un conjunto de datos x1 , x2 ,.... xn.... , es el valor que se encuentra en la posición central de todo el conjunto de datos ordenados en forma creciente , y se calcula dependiendo la disposición de los mismos.

• Datos individuales : Si el numero de datos(n)  es impar , se toma el valor medio del conjunto , y si el numero de datos(n) es par  se realiza la semisuma entre los dos datos que se encuentran en la mitad del conjunto resultando la mediana.
• Datos individuales con frecuencias : Se divide el numero total de datos para dos , luego se clasifica el resultado obtenido en un cierto intervalo y se considera como mediana el dato del conjunto que pertenezca al intervalo mencionado.
• Datos agrupados con intervalos : Se aplica la siguiente formula :

-Moda : Se calcula para datos tanto cuantitativos como cualitativos , se obtiene considerando el valor de la variable que tiene mayor frecuencia .

Cabe recalcar que en un conjunto de datos puede haber mas de una moda.

2) Calculo de medidas de dispersión:

-Rango : Se calcula restando el valor mínimo del valor máximo. , tanto para datos individuales , agrupados o con frecuencia.

R= Xmax - Xmin 

-Varianza: Se calculo dependiendo la disposición de los datos :

• Datos individuales : Se aplica la siguiente formula:

• Datos individuales con frecuencia : Para determinarla aplicamos la siguiente formula:

-Desviación estándar : Se define como la raíz cuadrada de la varianza para datos individuales:

-Desviación típica : Se define como la raíz cuadrada de la varianza para datos individuales con frecuencia :

CLASE # 11

Lunes , 25 de mayo del 2016

1) Calculo de medidas de posición.

En esta clase , se realizo el estudio del calculo de medidas de posición , y respecto a esto se definieron términos como deciles , percentiles y cuartiles.
Entrando propiamente a la materia , se definieron a las medidas de posición como aquellas que dividen un conjunto de datos en grupos con el mismo numero de individuos ; para calcular este tipo de medidas es necesario que los datos estén ordenados de menor a mayor.

*Percentiles: Los percentiles se definen como los 99 valores que dividen una serio de datos en 100 partes iguales , porcentualmente corresponden al 1% , 2% , 3% ,...., 99 % .de los datos. Una observación respecto a esto es que la mediana coincide con el Percentil 50 ( P50).
Para calcular los percentiles ,

• En primer lugar se busca la clase en donde se encuentra k*N/100 , donde k= 1 ,2 , 3, ...., 99.
• Luego en caso de que los datos sean agrupados aplicamos la siguiente formula considerando la tabla de frecuencias , en especial la acumulada.

Donde :
Li : Representa el limite inferior de la clase donde se encuentra la mediana.
 N : Es la suma de las frecuencias absolutas.
Fi-1 : Es la frecuencia acumulada anterior a la clase mediana.
ai : Es la amplitud de la clase.

*Deciles : Los deciles son un tipo de medidas de posición que se definen como los nueve valores que dividen la serie de datos en 10 partes iguales ; en proporción , corresponden justamente al 10 %  , 20 % , 30 % ,.....,90 % de los datos. cabe recalcar que que el quinto decil ( D5 ) coincide con la mediana.
Para calcular los deciles se realiza lo siguiente :

• En primer lugar se busca la clase en donde se encuentra k*N/10 , donde k= 1 , 2 ,..., 9 , en la tabla de frecuencias acumuladas.
• Posteriormente aplicamos la siguiente formula:

Donde :

 Li : Representa el limite inferior de la clase donde se encuentra la mediana.

 N : Es la suma de las frecuencias absolutas.

Fi-1 : Es la frecuencia acumulada anterior a la clase mediana.

ai : Es la amplitud de la clase.

Gráficamente los deciles se pueden representar de la siguiente manera:

*Cuartiles : Los cuartiles son los 3 valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.

representan en forma porcentual los valores de 25% , 50% y 75% denotados como Q1 , Q2 Y Q3 respectivamente.

Para el calculo de los cuartiles se deben seguir las siguientes pautas :

1.-Ordenar los datos de menos a mayor.

2.-Buscamos el lugar que ocupa cada cuartil mediante la siguiente expresión: k*N/4 , donde k = 1,2,3.

3.-Ahora , para calcular los cuartiles en datos sin agrupar se deben realizar las siguientes consideraciones :

• Si el numero de datos es impar: se tiene por ejemplo: 

          

• Si el numero de datos es par : Se tiene por ejemplo :

En resumen , gráficamente los cuartiles los podemos representar de la siguiente manera :

*Diagrama de Cajas : El diagrama caja o bigotes es una representación visual que describe características importantes para realizar un análisis como por ejemplo dispersión y simetría.  

Estructuralmente consta de los tres cuartiles y los valores máximos y mínimos de los datos , sobre un rectángulo alineado vertical u horizontalmente.  

      

CLASE # 12

Miércoles , 25 de mayo del 2016

La presente sesión de clases , se realizo la revisión de las medidas de Forma como continuación a la temática del calculo de medidas para datos cuantitativos a excepción de la Moda (Mo).

Durante esta clase se estudió los siguientes temas:

1) Coeficiente de Asimetria (As)

Es un valor propiamente estadístico , que tiene como objetivo establecer la simetría de la distribución de los datos y se lo puede calcular por medio de la siguiente formula :

Una vez realizado el calculo , se procede a tomar en cuenta los siguientes aspectos para obtener una conclusión determinante , tras el análisis.

• Si As > 0 , entonces se dice que la distribución de datos es asimétrica a la derecha .
• Si As = 0 , entonces la distribución presenta simetría respecto a la media.
• Si As < 0 , entonces la distribución de datos es asimétrica a la izquierda respecto a la media.

2) Coeficiente de apuntamiento (Ap)

Es una medida de la forma , que consiste en el estudio de la proporción de la varianza que es explica por la combinación de datos extremos respecto a la media y los datos que bien pueden estar cerca o alejados de aquella.

Para calcular dicho coeficiente se aplica la siguiente formula:

Luego , tras obtener dicho valor , se realiza las siguientes observaciones para determinar una conclusión:

• Si Ap > 0 , la distribución se denomina Leptocurtica.
• Si Ap = 0 , la distribución se denomina Mesocurtica.
• Si Ap < 0 , la distribución es de tipo Platicurtica.

A continuación los tres gráficos que representan los tres tipos de distribuciones ya mencionadas:

3) Muestras Bivariadas.

Son aquellas muestras que se originan dado que existen casos en que los datos de las muestras miden dos características , siendo entonces importante determinar si existe alguna relación entre ellas.
Para realizar este tipo de ejercicios se suele denotar a las 2 características por medio de variables , X y Y , estableciendo de esta manera un función en donde Y depende de X para posteriormente representar un diagrama de dispersión , que nos lleva a suponer la tendencia que tiene la relación por medio de la gráfica formada por una serie de puntos.

4) Correlación.

La correlación es un factor que indica la dirección de una relación lineal y proporcionalidad entre dos variables estadísticas.
Profundizando en este concepto desde un punto de vista gráfico , puede evidenciarse los siguientes casos tras un análisis bivariado:

5) Covarianza muestral:

La covarianza muestral es una medida que nos permite cuantificar el nivel de relación entre dos variables . Para realizar dicho análisis se requiere determinar las desviaciones típicas tanto para X como para Y , después en base a esto propiamente la covarianza muestral definida como :

 6) Coeficiente de correlación :

El coeficiente de correlación es una cifra que permite cuantificar el grado de correlación lineal.
Matemáticamente se define como el cociente entre la covarianza y el producto de las desviaciones típicas de ambas variables , se simboliza con la letra " r ''  y varia entre 1 y -1.

Una vez obtenido el coeficiente de correlación se procede a tomar en cuenta los siguientes enunciados :
- Si r tiene un valor cercano 1 , la correlación es fuerte positiva.
-Si r tiene un valor cercano a -1 , la correlación es fuerte negativa.
-Si r tiene un valor cercano a 0 , la correlación es debió o bien no existe correlación entre las variables.
Mediante dichos enunciados se puede comprender el siguiente gráfico:

5) Matriz de varianzas y covarianzas.

Una matriz de varianzas-covarianzas es una matriz cuadrada que contiene las varianzas y covarianzas asociadas con diferentes variables , los elementos de la diagonal contienen las varianzas de las variables , mientras que en la otra diagonal se encuentran las covarianzas.

 

6) Matriz correlación. 

La matriz de correlación nos indica como están relacionadas cada una de las variables con otra variable , su diagonal siempre contendrá el valor de 1 , si tiene un valor de 0 nos indicara que no tiene ninguna relación con esa variable , o por lo menos no lineal , es decir que puede tener una relación cuadrática o de otro grado.

.

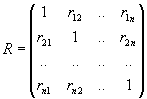CLASE # 13

Lunes , 30 de mayo del 2016

En esta clase iniciamos formalmente con el estudio de los FUNDAMENTOS DE LA TEORÍA DE LA PROBABILIDAD , mas específicamente con el tema correspondiente a formulas de contéo.

Inicialmente se definió al principio básico de conteo como :

"Un grupo tiene m elementos y otro grupo tiene n elementos , entonces existe mxn formas diferentes de tomar un elemento del primer grupo y otro elemento del segundo grupo'' (Rodriguez , 2007 )

Se estudio los siguientes ejemplos relacionados al tema :

Y para ir desde A hasta C existen 2x3=6 , 6 formas diferentes.

PERMUTACIONES.-

Se definen como los arreglos diferentes que se pueden hacer con los elementos de un grupo , a diferencia de las combinaciones en este caso se debe considerar el orden de los elementos incluidos.

En cuanto a formulas se definen las siguientes:

Dentro de las permutaciones , se analizó casos especiales como :

PERMUTACIONES CON TODOS LOS ELEMENTOS.-

La permutación con todos los elementos del conjunto se define como :

Un ejemplo de este caso es el siguiente:

  120 formas distintas para ensamblar la maquina.

ARREGLO CIRCULAR.-

Si se considera un grupo con n elementos diferentes . Un arreglo circular se define como una permutación con todos los elementos del grupo en donde el primero y el ultimo se encuentran enlazados , fijando un elemento para que los otros puedan intercambiarse.

Matemáticamente se define como:

Donde n es el numero total de elementos. 

Un ejemplo para este caso es el siguiente:

PERMUTACIONES CON ELEMENTOS REPETIDOS.-

Si se un total de n elementos , n1 fuesen repetidos , entonces los arreglos tendrían formas idénticas cuando se considera el orden de los n1 elementos repetidos . Entonces generalizando dicho concepto se tiene que :

COMBINACIONES.-

Se define a las combinaciones como los arreglos que se pueden hacer con los elementos de un conjunto , teniendo en cuenta que el orden de los elementos en este caso no es de mayor interés.

Matemáticamente las combinaciones se definen como :

Ejemplo 1. En un grupo de 15 personas , 7 leen la revista A , 5 leen la revista B , y 6 ninguna revista. Encuentre la cantidad de personas que leen al menos una revista.