CLASE # 23
DISTRIBUCIÓN BINOMIAL :
Esta distribución es una de las mas importantes , corresponde a experimentos parecidos a los de que siguen una distribución de Bernoulli , a diferencia de que en este tipo de distribución es de interés la variable aleatoria que representa la cantidad de éxitos que se obtienen en cierto experimento.
Características de la distribución binomial :
- La cantidad de ensayos n , que se realizan es finita.
- Cada ensayo cuenta con únicamente dos resultados posibles : Éxito o fracaso.
- Todos los ensayos realizados corresponden a eventos independientes.
- La probabilidad p de obtener "éxito" en cada ensayo permanece constante.
Algunos ejemplos muy comunes en los que usualmente se emplean la distribución binomial para su resolución son los siguientes:
- Ejemplos que involucran el calculo de la probabilidad de una cierta cantidad de artículos defectuosos de una muestra tomada al azar en una fabrica.
- Determinar la probabilidad de la cantidad de personas que están a favor de un candidato , una muestra de personas elegidas de cierta población.
Previo a la definición de distribución Binomial se definen los siguientes parámetros:
X: Representa la variable aleatoria discreta que da a conocer la cantidad de ensayos que corresponden a éxitos.
x: 0,1,2,3,...n. Valores que puede tomar X.
p: Probabilidad de que el resultado de cada ensayo sea exitoso.
Matemáticamente y considerando los parámetros descritos , definimos a la Distribución Binomial de la siguiente manera :
Su MEDIA Y VARIANZA se definen de la siguiente manera:

Ejemplo de distribución binomial:

Gráfica que sigue una DISTRIBUCIÓN BINOMIAL:
DISTRIBUCIÓN BINOMIAL NEGATIVA :
Similar a la distribución binomial , se caracteriza porque los ensayos son independientes , cada ensayo tiene únicamente dos resultados posibles y la probabilidad de que cada ensayo tenga un resultado favorable es constante.
Sin embargo su caracteristica mas importante es que la variable de interés en este caso es la cantidad de ensayos que se realizan hasta obtener un numero requerido de éxitos (K).
Teniendo en cuenta lo mencionado , definimos a la DISTRIBUCIÓN BINOMIAL NEGATIVA así :

La MEDIA Y VARIANZA que corresponden a este tipo de distribución es la siguiente:

Ejemplo en el que se aplica la Distribución Binomial negativa:

DISTRIBUCIÓN GEOMÉTRICA :
Es una variante o caso especial de la Distribución Binomial negativa , cuando k=1 . En este caso interesa conocer la probabilidad respecto a la cantidad de ensayos que se realizan hasta obtener el primer "éxito".
Se define de la siguiente forma :
X: Variable aleatoria discreta con distribución geométrica.
x: 1,2,3,....n . Valores que puede tomar X.
p: Probabilidad constante de éxito en cada ensayo.
Característicamente la expresión que representa a la DISTRIBUCIÓN GEOMÉTRICA es la siguiente:
La MEDIA Y VARIANZA de esta distribución se encuentran definidas de la siguiente forma:

Ejemplo correspondiente a Distribución Geométrica:

CLASE # 24
DISTRIBUCIÓN HIPERGEOMÉTRICA :
Esta distribución esta netamente relacionada con los experimentos estadísticos que consisten en tomar una muestra sin reemplazo de un conjunto finito que contiene elementos considerados "éxitos" mientras que los demás se consideran "fracasos".
Al mencionar la frase "Tomar una muestra sin reemplazo" nos referimos a que los elementos son tomados uno a uno , sin devolverlos , es decir alterando el numero inicial de individuos que conforman la muestra.
La distribución hipergeometrica se define de la siguiente manera:
La MEDIA Y VARIANZA relacionadas a este tipo de distribución , se denotan así :
Ejemplo correspondiente al tema tratado:
DISTRIBUCIÓN DE POISSON :
La DISTRIBUCIÓN DE POISSON es un método probabilista alternativo , pues nos permite determinar la probabilidad correspondiente a un numero de éxitos que se obtendrían en una región o intervalo de tiempo establecido , siempre y cuando se conozca el numero promedio de éxitos que ocurren.
Este método debe cumplir las siguientes condiciones:
- El numero de éxitos que ocurren en la región o intervalo es independiente de lo que ocurre en otra región o intervalo.
- La probabilidad de que cierto resultado ocurra en una región o intervalo pequeño es igual para todos los intervalos o regiones de igual magnitud.
- La probabilidad de que mas de un resultado ocurra en una región no es significativa.
Definición de la DISTRIBUCIÓN DE POISSON:
MEDIA Y VARIANZA de la Distribución de Poisson:
Ejemplo resuelto empleando este tipo de distribución :

CLASE # 25
VARIABLES ALEATORIAS CONTINUAS:
"Una variable aleatoria X es continua si su función de distribución es una función continua.
En la práctica, se corresponden con variables asociadas con experimentos en los cuales la variable medida puede tomar cualquier valor en un intervalo: mediciones biométricas, intervalos de tiempo, áreas, etc." www.ub.edu.
FUNCIÓN DE DENSIDAD DE PROBABILIDAD:
La probabilidad de una variable aleatoria continua puede especificarse siempre y cuando exista una función llamada función de densidad de probabilidad , en la cual una vez graficada , el área bajo la curva descrita cumpla los requerimientos para poder considerarse una medida del valor de probabilidad.
Matemáticamente esta función se define de la siguiente forma:

La gráfica que la representa es la siguiente:
Respecto a sus propiedades , destacan las siguientes:

Similar al caso de variables aleatorias discretas se puede definir una función de distribución acumulada , denominada para las variables aleatorias continuas como FUNCIÓN DE DISTRIBUCIÓN.
Definición formal:

Luego , esta función de probabilidad debe cumplir ciertas condiciones (detalladas a continuación) para ser considerada como tal:

MEDIA Y VARIANZA DE VARIABLES ALEATORIAS CONTINUAS :
Matemáticamente se definen de la siguiente forma:

PROPIEDADES DE LA MEDIA Y VARIANZA:

CLASE # 26
DISTRIBUCIONES DE PROBABILIDADES CONTINUAS:
El objetivo relacionado a este tipo de distribuciones es obtener una formula matemática f(x) para determinar los valores de probabilidad de la variable aleatoria X.
DISTRIBUCIÓN UNIFORME CONTINUA :
Este tipo de distribución corresponde a una variable aleatoria continua cuyos valores tienen igual valor de probabilidad.
Formalmente se define como :









CLASE # 27
Lunes , 18 de Julio del 2016.
DISTRIBUCIÓN GAMMA:
Es un tipo de distribución continua cuya definición es la siguiente:

Aspectos importantes relacionados a este tipo de distribución:

Gráfica de la Distribución Gamma:

Su MEDIA Y VARIANZA son las siguientes:
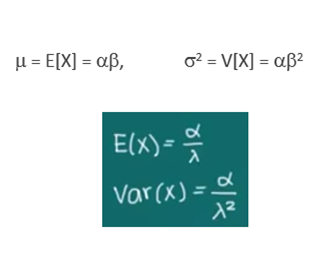



Miércoles , 20 de Julio del 2016.
DISTRIBUCIÓN BETA :
En el campo de la estadística , La distribución Beta es un distribución de probabilidad continua con dos parámetros definidos como a y b , cuya función de densidad esta definida para valores que comprendan el intervalo entre 0 y 1 y se define como :

![{\displaystyle E[X]={\frac {a}{a+b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eac047f8695980468991554cd84bc120baee9610)
![{\displaystyle V[X]={\frac {ab}{(a+b+1)(a+b)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e068a3e9b972bb4e45488fed901f986897af133)


Lunes , 25 de Julio del 2016.







Miércoles , 27 de Julio del 2016.
DISTRIBUCIÓN F :
Es una distribución muy útil que nos permite realizar inferencias con las varianzas de dos poblaciones normales usando los datos de las varianzas de dos muestras aleatorias independientes con la siguiente definición:



El objetivo relacionado a este tipo de distribuciones es obtener una formula matemática f(x) para determinar los valores de probabilidad de la variable aleatoria X.
DISTRIBUCIÓN UNIFORME CONTINUA :
Este tipo de distribución corresponde a una variable aleatoria continua cuyos valores tienen igual valor de probabilidad.
Formalmente se define como :

Gráficamente se representa de la siguiente forma:
Las formulas de la VARIANZA y LA MEDIA de este tipo de distribución son las siguientes:

Ejemplo relacionado a este tipo de distribución :
DISTRIBUCIÓN NORMAL :
La distribución normal es uno de los conceptos estadísticos modernos mas importantes , pues se utiliza para describir el comportamiento aleatorio de muchos procesos que ocurren en la naturaleza y también realizados por el hombre.
Matemáticamente se define de la siguiente manera:

Donde :
- t representa a la variable aleatoria con media u y desviación típica sigma.
Gráficamente se representa de la siguiente forma:

Para determinar las probabilidades generalmente se usa una tabla estandarizada , descrita a continuación :
Donde en la primera columna se encuentra el primer entero y decimal , mientras que en la primera fila el valor centesimal , que complementa la probabilidad del valor a encontrar.
ESTANDARIZACIÓN DISTRIBUCIÓN NORMAL :
También conocido como TIPIFICACION de la variable aleatoria con distribución binomial "X" , es un cambio de variable que nos facilita el calculo de probabilidades , pues reduce el valor inicial correspondiente a la variable X , convirtiéndolo en una cifra relacionada con la variable Z caracterizada porque sigue una distribución normal , cuya media es igual a 0 y desviación típica igual a 1.
Conceptualmente se define así:

Ejemplo :
CLASE # 27
DISTRIBUCIÓN GAMMA:
Es un tipo de distribución continua cuya definición es la siguiente:
Donde Alfa y Beta son los parámetros para este modelo.
Aspectos importantes relacionados a este tipo de distribución:
Gráfica de la Distribución Gamma:
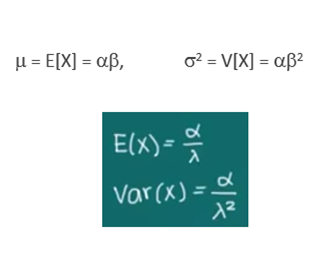
DISTRIBUCIÓN EXPONENCIAL:
Se define como un caso particular de la Distribución Gamma , pues se aplica cuando se considera alfa igual a 1.
Su definición matemática es la siguiente:
Características:
Ejemplo:
CLASE # 28
DISTRIBUCIÓN BETA :
En el campo de la estadística , La distribución Beta es un distribución de probabilidad continua con dos parámetros definidos como a y b , cuya función de densidad esta definida para valores que comprendan el intervalo entre 0 y 1 y se define como :

Ademas posee MEDIA Y VARIANZA como las demás distribuciones ; sus formulas son respectivamente las siguientes :
![{\displaystyle E[X]={\frac {a}{a+b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eac047f8695980468991554cd84bc120baee9610)
![{\displaystyle V[X]={\frac {ab}{(a+b+1)(a+b)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e068a3e9b972bb4e45488fed901f986897af133)
Gráficamente se caracteriza de la siguiente manera:

Ejemplo de una aplicación de la DISTRIBUCIÓN BETA:
CLASE # 29
DISTRIBUCIÓN T O STUDENT :
La distribución T , también conocida como Distribución Student , es una función de probabilidad de tipo simétrica y cuya gráfica se asemeja a la de una campana.
Este tipo de distribución es muy ventajosa en algunos casos , uno de ellos y el mas importante es que cuando se tiene una muestra con un numero de individuos menor a 30 , cuya caracteristica es que sigan una distribución normal con un valor de media pero sin un valor de varianza conocido , es el estadístico ideal para estimar valores de media , varianza , realizar pruebas de hipótesis o muestreo estadístico.
Para definir dicha distribución , se requiere conocer un valor X que representa una media población , y un valor S al cuadrado que representa la varianza correspondiente a la misma población , entonces matemáticamente la distribución T se define de la siguiente manera:
Gráficamente esta distribución se representa así :
Donde x representa los valores de probabilidad a determinar , mientras que en el eje Y los distintos valores obtenidos luego de aplicar la función de densidad f(x).
Otra ventaja que presenta este tipo de distribución , es que se puede emplear tablas para la determinación de probabilidades , siempre y cuando se consideren los grados de libertad definidos como v=n-1 , donde n representa el numero total de individuos que conforman la población.
A continuación una pequeña porción de la tabla correspondiente a esta Distribución:
DISTRIBUCIÓN JI-CUADRADO :
Esta distribución es bastante especial , pues se la obtiene de la Distribución Gamma , su gráfica se caracteriza por tener forma de campana con sesgo positivo ; en cuanto a las ventajas que presenta , es muy importante pues es muy útil en problemas de muestreo que involucren poblaciones que sigan una distribución normal.
Se define simbólicamente considerando parámetros como el numero de individuos que conforman la población , la varianza poblacional y la varianza muestral.
Su función de densidad es la siguiente:

donde T representa la distribución Gamma.
Como estimador estadístico se suele definir de la siguiente forma:
Formula utilizada para realizar ejercicios que involucren Bondad de ajuste.
En cuanto a su gráfica:
CLASE # 30
DISTRIBUCIÓN F :
Es una distribución muy útil que nos permite realizar inferencias con las varianzas de dos poblaciones normales usando los datos de las varianzas de dos muestras aleatorias independientes con la siguiente definición:
Ademas se consideran dos grados libertad , los mismos que corresponden a los dos grupos o muestras que se están evaluando.
Ejemplo:
No hay comentarios.:
Publicar un comentario